　
　
明日の授業にほんのちょっとのデジタルコンテンツ！！
詳しい使い方はこちら　

小単元	時間	学習活動
小単元	時間	学習活動	課題発見	体験を想起させる　比べる、分かりなおす	見ることができない体験できない	演示、正確な動き　よくない方法、失敗例	繰り返しドリル
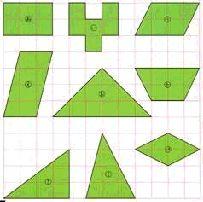
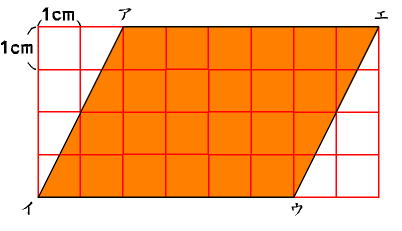
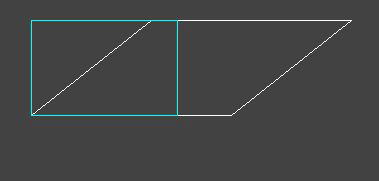
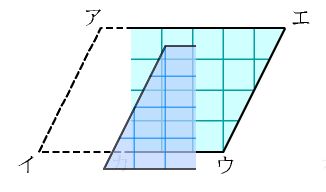
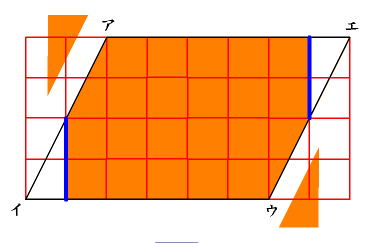
課題設定・平行四辺形の面積	１	学習の動機づけ平行四辺形の求積の仕方を考える	・同じ面積の図形を見つけようとする	・平行四辺形を変形すると長方形になることがわかる	・どんな平行四辺形でも同じように面積を求められることがわかる	・平行四辺形の面積の求め方を理解する	・平行四辺形を変形して長方形にすることができる


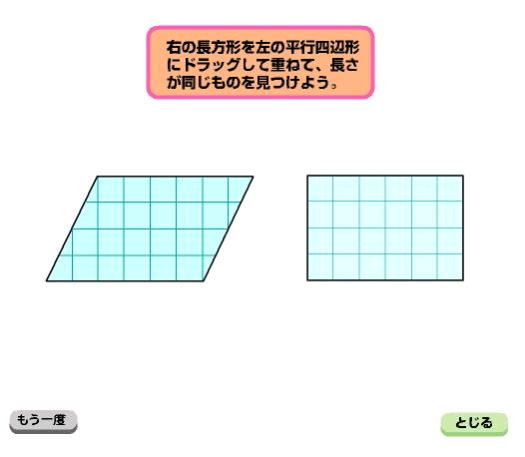
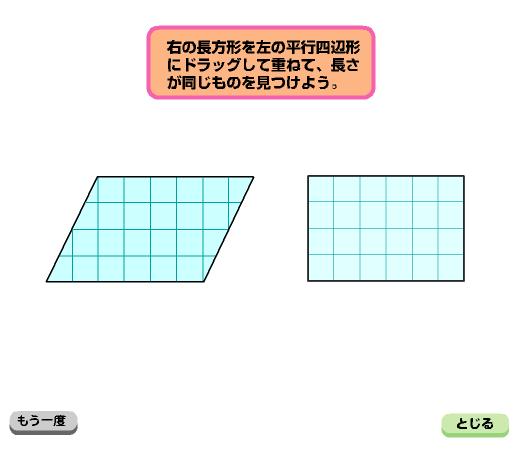
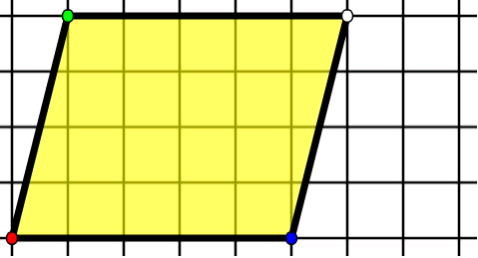
	２	平行四辺形の求積の公式を考える	・どんな平行四辺形でも面積の公式で求められるか調べようとする	・平行四辺形を変形したことにより、公式にすることができることがわかる	・どんな平行四辺形でも面積の公式で求められることがわかる	・平行四辺形の面積の公式を深く理解する	・底辺に対する高さがどこかわかり、面積を求めることができる


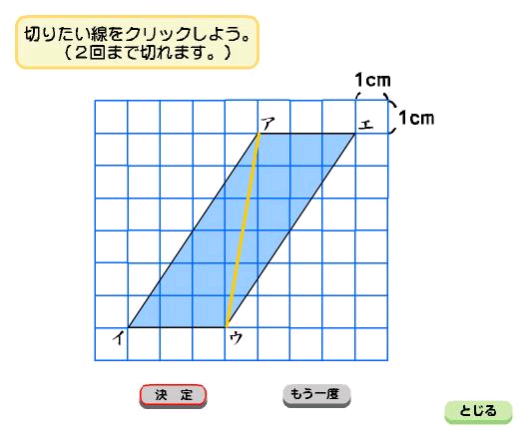
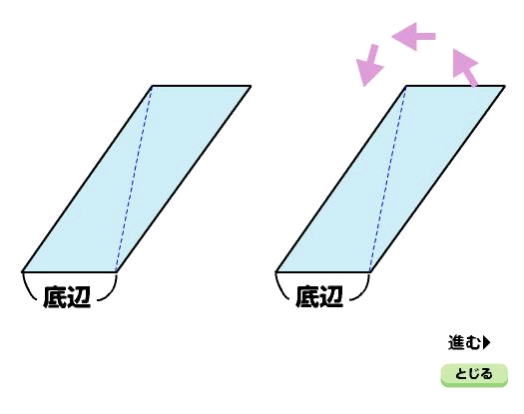
	３	高さが外にある平行四辺形の求積の公式を考える	・高さが外にあるどんな平行四辺形でも同じように面積を求められるか調べようとする	・高さが外にある平行四辺形を変形すると長方形になることがわかる	・どんな高さが外にある平行四辺形でも同じように面積を求められることがわかる	・高さが外にある平行四辺形の面積の求め方を理解する	・底辺に対する高さがどこか見つけることができる


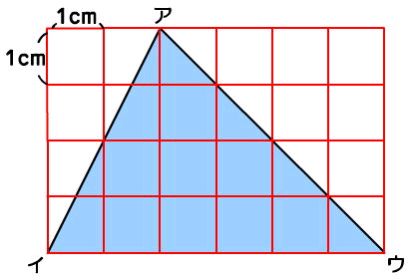
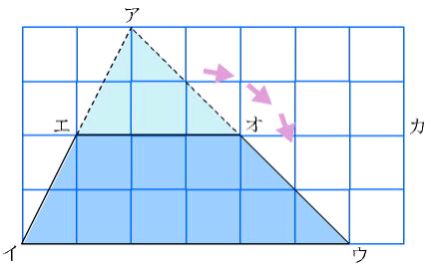
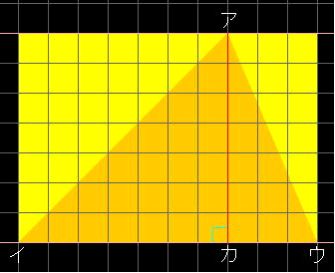
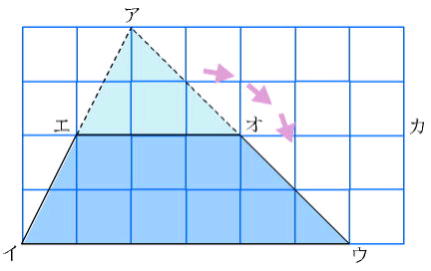
三角形の面　積	４	鋭角三角形の求積の仕方を考える	・どんな鋭角三角形でも同じように面積を求められるか調べようとする	・鋭角三角形を２つ組み合わせると、平行四辺形になることがわかる・鋭角三角形を変形すると長方形になることがわかる	・どんな鋭角三角形でも同じように面積を求められることがわかる	・鋭角三角形の面積の求め方を理解する	・底辺に対する高さがどこか見つけることができる


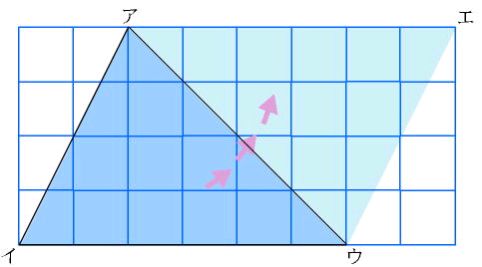
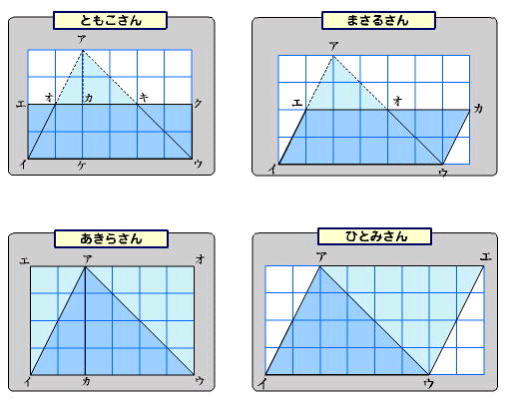
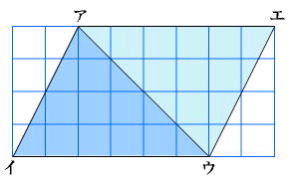
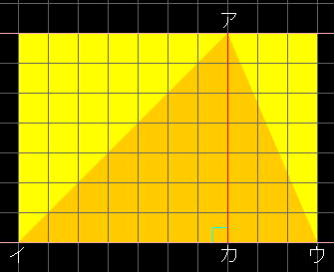
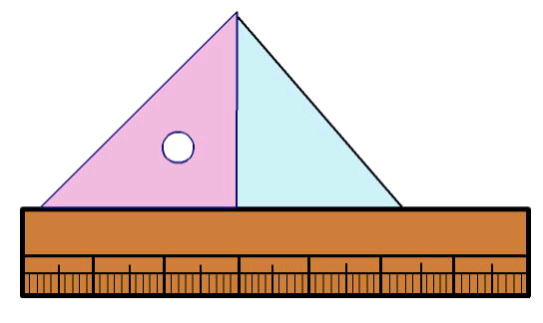
	５	鋭角三角形の求積の公式を考える	・どんな鋭角三角形でも面積の公式で求められるか調べようとする	・鋭角三角形を変形したことで、公式化できることがわかる	・どんな鋭角三角形でも面積の公式で求められることがわかる	・鋭角三角形の面積の公式を深く理解する	・鋭角三角形をあわせたり移動したりして長方形に変形できる


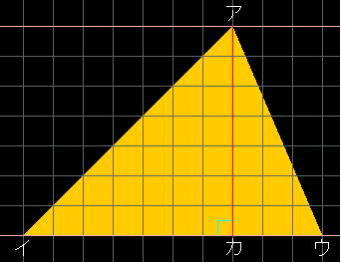
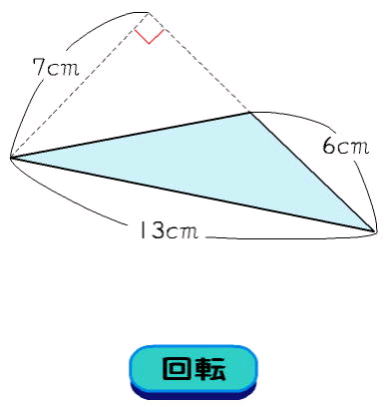
	６	鈍角三角形の求積の仕方を考える	・どんな鈍角三角形でも同じように面積を求められるか調べようとする	・鈍角三角形を２つ組み合わせたり、変形すると、平行四辺形になることがわかる	・どんな鈍角三角形でも同じように面積を求められることがわかる	・鈍角三角形の面積の求め方を理解する	・底辺に対する高さがどこか見つけることができる


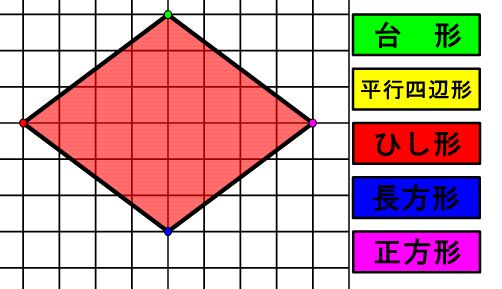
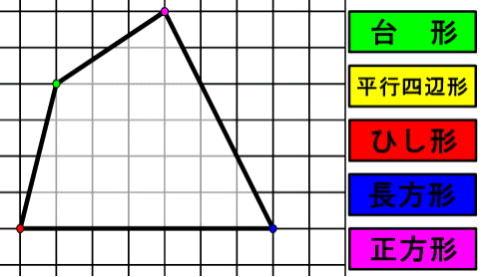
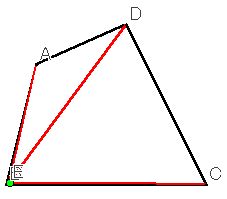
発展学習	発展１	一般四角形の求積の仕方を工夫する	・どんな四角形でも同じように面積を求められるか調べようとする・どんな多角形も同じように面積を求められるか調べようとする	・四角形の面積を２つの三角形にわける求め方を理解する	・どんな四角形でも同じように面積を求められることがわかる・どんな多角形も同じ考えで面積を求められることがわかる	・２つの三角形にわけて四角形の面積の求め方を理解する	・四角形を２つの三角形に分けるとともに、底辺に対する高さを見つけることができる


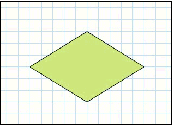
	発展２	ひし形の求積の仕方を考え、公式を考える	・どんなひし形でも同じように面積を求められるか調べようとする	・ひし形を変形すると長方形になることがわかる	・どんなひし形でも同じように面積を求められることがわかる	・ひし形の面積の求め方を理解する	・たて・横がどこか見つけることができる


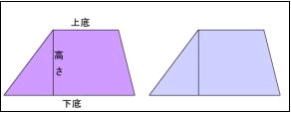
	発展３	台形の求積の仕方を考え、公式を考える	・どんな台形でも同じように面積を求められるか調べようとする	・台形を２つ組み合わせると平行四辺形になることをがわかる・鋭角三角形を変形すると長方形や平行四辺形になることがわかる	・どんな台形でも同じように面積を求められることがわかる	・台形の面積の求め方を理解する	・上底・下底・高さがどこか見つけることができる